ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Spanish Language Videos 26 videos
Pobre Batman, la probabilidad básica está haciendo su vida más difícil. Solamente cuando el ha tomado al pingüino , lo ha encerrado tras las r...
¿Has estado pasando todo tu tiempo alrededor números irracionales? Están cheveres del todo, y definitivamente interesantes, pero; ¿no valoras...
Algebra y Funciones, Problema de la Palabra 201 Views
Share It!
Description:
La lanza necesita velocidad. Afortunadamente, ella solamente tiene una bicicleta, ella no quiere poner en peligro cada vida humana. Nosotros no envidiamos cualquier caracol que toma en su camino.
Transcript
- 00:10
Lanza montaba su bicicleta a la escuela a pedaleando a una velocidad promedio de 12
- 00:17
millas por hora. Cuando andaba en su bicicleta de vuelta a
- 00:20
casa a paso lento de 10 kilómetros por hora, que le llevó un extra de 15 minutos.
- 00:31
¿A qué distancia está su escuela desde su casa?
- 00:37
A - 1.25 millas? B - 1.5 kilómetros?
Full Transcript
- 00:41
C - 12 millas? D - 13.5 millas?
- 00:44
E - 15 millas?
- 00:45
Conoce a Lance. Él era un miembro del equipo juvenil de ciclismo
- 00:51
olímpico de los Estados Unidos. Hasta que sus calificaciones en matemáticas
- 00:56
empezaron a caer y he hizo que sus padres usaran el martillo. Ahora la moto es sólo
- 01:03
para el transporte. Ah, bueno. Tal vez él pueda ganar una medalla
- 01:07
de oro en "llegar a la escuela a tiempo."
- 01:11
Como usted sabe, un día completo de escuela realmente puede minar su energía.
- 01:16
Así que no es sorpresa que Lance este cansado de camino a casa.
- 01:23
La pregunta es cual es la diferencia de que esos 2 millas por hora.
- 01:27
Eso le cuesta a Lance un extra de 15 minutos. Tiempo que podría haber sido bien gastado
- 01:34
haciendo su tarea de matemáticas. O bien, viendo Sportscenter, o lo que sea.
- 01:39
Bueno, es hora de fórmula. Hay una igualdad básica aquí - desde que
- 01:46
Lance está viajando a la misma distancia en ambos sentidos.
- 01:50
Es justo que lo llevaba un poco más en el camino de vuelta a casa.
- 01:56
Levante los pies, muchacho.
- 01:58
Así que vamos a llamar a las 12 millas por hora promedio de Lance tomó para llegar a
- 02:04
la escuela "12x" ... ... Y el tiempo que le tomó llegar a casa
- 02:10
"10x + 0.25" ... ... El 10 veces representa su velocidad media
- 02:15
en el camino a casa y "0,25" representa la cuarta parte de más de una hora que le lleva
- 02:28
pedalear su camino a casa.
- 02:29
Cuando distribuimos ... Vemos que ... 12x = 10x + 2,5
- 02:31
Quita 10x de ambos lados ... Y obtenemos 2x igual 2,5.
- 02:40
Divide ambos lados entre 2 y tenemos un valor para nuestra "x" - 1,25 horas.
- 02:59
Eso está bien y todo ... pero estamos resolviendo para la distancia.
- 03:01
Así se multiplica el tiempo que le tomó por su velocidad media. Lo que se muestra
- 03:08
mediante la adopción de 12 millas por hora multiplicado por 1,25 horas, lo que nos da
- 03:13
nuestra respuesta final ... 15 millas.
- 03:15
Parece que la respuesta es la opción E - Lance tiene un trayecto de 15 km a la escuela.
- 03:26
... Nos cansamos de conducir el coche durante 15 kilómetros.
- 03:30
Está bien, Lance. No te culpo por ser un poco lento.
Related Videos
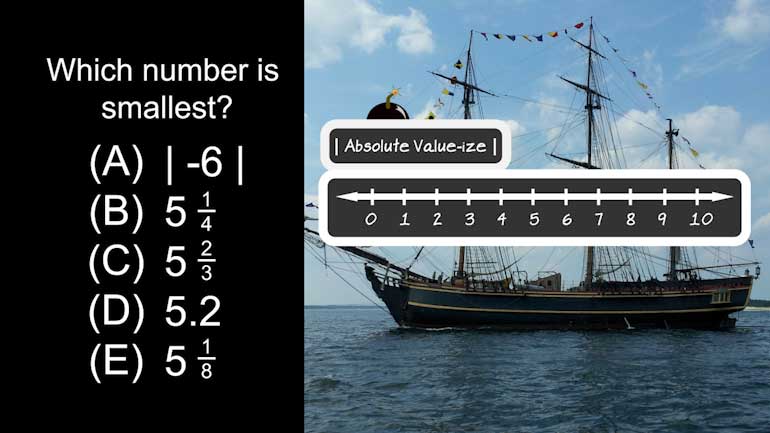
ACT Math: Pre-Algebra Drill 2, Problem 3. Which of the following numbers is smallest?
ACT Math: Pre-Algebra Drill 2, Problem 4. Which of the following numbers is largest?
SAT Math: Algebra and Functions Drill 1, Problem 2. Based on the data in the table, what is the maximum heart rate for the average 22-year-old?
Who wants to be a millionaire? In this video, learn about compound interest, interest rates, and the compound interest formula. You'll be buying th...
ACT Math: Pre-Algebra Drill 5, Problem 2. If a and b are prime numbers, how many factors does ab have?