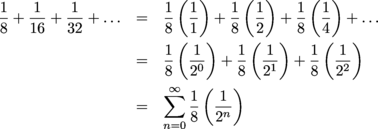Answer
(a) We can rewrite the series so the terms are fractions whose denominators are powers of 2:
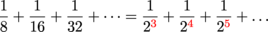
From here it makes sense to view the series as starting at n = 3 and having general term
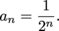
Then we can write the series in sigma notation as

(b) Way 1: We already saw that we can rewrite the series as
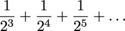
In order to think of the first term as using n = 2 instead of n = 3, we can break up the denominators like this:

Then we can write the series as
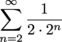
Way 2: Pull out  from each term and rewrite the series as
from each term and rewrite the series as

This can be viewed as a series with general term
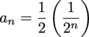
starting at n = 2. We write the series in summation notation as
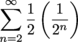
This is equivalent to what we got with Way 1.
(c) Way 1: In order to start at n = 1, we can break up the denominators like this:

Then we can write the series as

Way 2: This is very similar to (b), except that we'll pull out  from each term so we can view the remaining powers of 2 as starting at n = 1.
from each term so we can view the remaining powers of 2 as starting at n = 1.
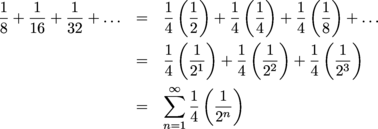
(d) Way 1: Rewrite the series so the denominator of term an has a factor of 2n, starting at n = 0:

Then we can write the series as

Way 2: If we want the first term to involve 2 with an exponent of 0, we need to factor out  from every term:
from every term: