Answer
f (x) = x2ex – 4ex
Rewrite f so we can tell what's going on.
f (x) = ex(x2 – 4) = ex(x – 2)(x + 2).
This is zero when x = ± 2, so the x-intercepts are (2, 0) and (-2, 0). The y-intercept is (0,-4).
The derivative of f is
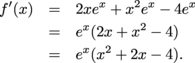
We need to use the quadratic formula to find the roots of (x2 + 2x – 4), which will be the only places where f ' is zero.

The critical points are

and

The second derivative of f is

Again, we need to use the quadratic formula. We need to find the roots of (x2 + 4x – 2), since these are the places f " will be zero.

Since the sign of f" does change at these x-values, these are both inflection points of f. We will find their full coordinates.
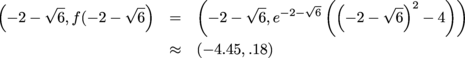

We need to cheat a little on the labeling, because the exact coordinates are so awful.