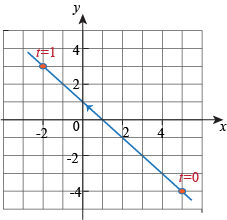
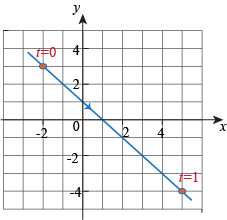
Going from left to right we put t = 0 at (-2, 3) and t = 1 at (5, -4).
First look at x and t. When t = 0 we have x = -2 and when t = 1 we have x = 5.
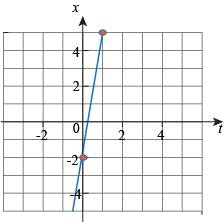
The intercept is -2 and the slope is 7, therefore x(t) = -2 + 7t.
Now look at y and t. When t = 0 we have y = 3 and when t = 1 we have y = -4.
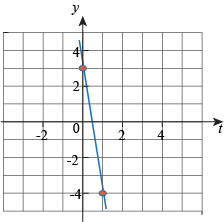
The intercept is 3 and the slope is -7, therefore
y = 3 – 7t.
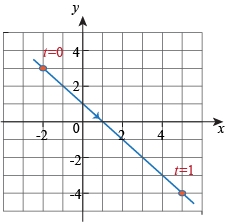
Going from right to left we put t = 0 at (5, -4) and t = 1 at (-2, 3).
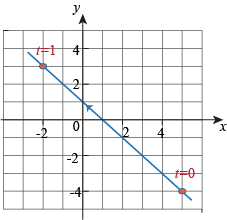
First look at x and t. When t = 0 we have x = 5 and when t = 1 we have x = -2.
The intercept is 5 and the slope is -7, therefore
x(t) = 5 – 7t.
Now look at y and t. When t = 0 we have y = -4 and when t = 1 we have y = 3.
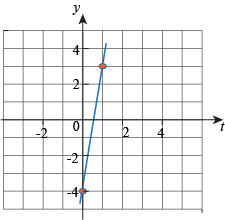
The intercept is -4 and the slope is 7, therefore
y(t) = -4 + 7t.
There are (at least two) ways to parametrize the line segment that connects the points (-2, 3) and (5,-4).
We can take either of the parametrizations we found in the previous problem and restrict t.
One possibility is
x(t) = -2 + 7t
y(t) = 3 – 7t
0≤ t ≤ 1
which traces the line segment from left to right:
Another possibility is
x(t) = 5 – 7t
y(t) = -4 + 7t
0≤ t ≤ 1
which traces the line segment from right to left:
,
the equation for x is
x(t) = 40t. 
so
the equation for y is
.
.
.