Answer
The denominator factors as
-2x2 + 7x + 15 = (2x + 3)(5 – x)
or as
-2x2 + 7x + 15 = (-2x – 3)(x – 5).
We'll go with
-2x2 + 7x + 15 = (2x + 3)(5 – x)
first. Then the decomposition will look like
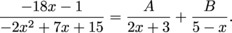
Add the partial fractions and set the resulting numerator equal to the original numerator:
-18x – 1 = A(5 – x) + B(2x + 3).
Take x = 5 and solve for B:
-18x – 1 = A(5 – x) + B(2x + 3)
-18(5) – 1 = A(5 – 5) + B(2(5) + 3)
-91 = 13B
-7 = B
Take x = 0 and solve for A:
-18x – 1 = A(5 – x) + B(2x + 3)
-18(0) – 1 = A(5 – 0) + (-7)(2(0) + 3)
-1 = 5A – 21
4 = A
The decomposition is
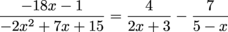
If instead we had started by factoring the denominator as
-2x2 + 7x + 15 = (-2x – 3)(x – 5)
then the decomposition would look like
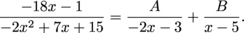
Add the partial fractions and set the resulting numerator equal to the original numerator:
-18x – 1 = A(x – 5) + B(-2x – 3).
Set x = 5 and solve for B:
-18x – 1 = A(x – 5) + B(-2x – 3)
-18(5) – 1 = A(5 – 5) + B(-2(5) – 3)
-91 = -13B
7 = B
Set x = 0 and solve for A:
-18x – 1 = A(x – 5) + B(-2x – 3)
-18(0) – 1 = A(0 – 5) + 7(-2(0) – 3)
-1 = -5A – 21
20 = -5A
-4 = A
Then the decomposition looks like this:
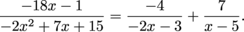
While these two answers may look different, they are in fact the same. If we multiply each term of our first answer by 1, we get
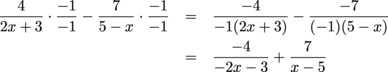
which is the same as our second answer.