The Basics - At A Glance

What is an exponential function anyways? There is one big thing to remember, the x is in the exponent. It doesn't necessarily have to be an x, it can be another variable.

These are all examples of exponential functions:

y = 5^x
y = 3(0.5)^x
f(x) = 2.9(3)^x
f(t) = e^t

Don't get confused about the function notation. If you remember back to Algebra 1 and Algebra 2, f(x) is just the dependent variable which stands for y.

Exponential functions are found in everyday life. Some exponential functions help calculate loans and savings accounts. Some functions calculate the population growth of a city. And some functions calculate the amount of mildew that will eventually take over your kitchen sink. May the bleach be with you.

General exponential functions are in the form:

y = ab^x
f(x) = ab^x

where a stands for the initial amount, b is the growth factor (or in other cases decay factor) and cannot also be = 1 since 1^x power is always 1. Notice the second equation was put in function notation, get used to seeing it both ways!

Exponential growth functions have b > 1, while exponential decay functions have b < 1. Also, the a value can tell us if the exponential curve is concave up (opening upwards) or concave down (opening downwards). If the a value is a positive number, the function will be concave up. If the a value is a negative number, the function will be concave down.

Sample Problem

It's 2095 and cloning technology is now upon us. If our technology was advanced enough, we could clone ourselves. We might have a problem on our hands.

Assume that human cloning is a thing that is happening.

Let's say that each day, each clone would clone themselves. To build this exponential function, the amount of clones would double each day . Our function would look like this:

f(x) = 2^x

where f(x) is the number of clones and x is the number of cloning days that took place

To find the number of clones of yourself after 10 cycles, we can simply substitute a 10 for the x.

f(10) = 2¹⁰ = 1024

That means there would be 1024 copies of yourself after 10 days! Hopefully you stocked up on deodorant.

Sample Problem

Some exponential functions can calculate the demise of the human race by the zombie apocalypse. It could start with one infection in one house. Yikes. Suppose a strange contagious virus began from a mutated gene. If one person was infected, they would die and the virus would take over their brain functions and their desire to eat anything living. The virus then would exponentially spread zombie to person, by a scratch or a bite, and new zombies would be created.

We could calculate the number of people that would be zombies after a time period with an exponential function like this:

f(t) = 2.1(4.9)^t

where t is time in days and f(t) is the number of zombies that are "alive."

Let's graph this function and look at what happens over a certain time:

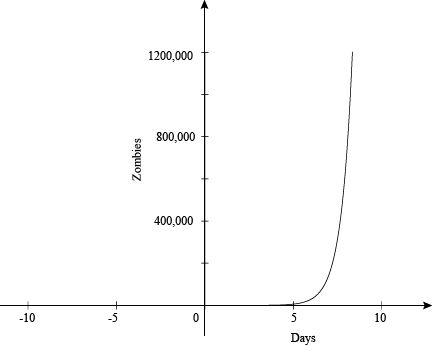
Notice the number of zombies increases without bound, even after only a few short days. Long story short, earth, we have a problem. There are zombies everywhere! This type of exponential graph is called exponential growth. Not only can the graph tell us that, but if you look at the original equation, we can tell it is an exponential growth equation. How? Since the general form of an exponential equation is:

f(x) = ab^x

Our zombie apocalypse equation has a = 2.1 and b = 3.05. Exponential growth functions have a b > 1. Also the a value is positive which shows a concave up graph. Can't zombies learn how to control themselves? There's got to be some type of medicine they can take to calm their need of feeding on people. Get ahold of yourselves, zombies.

Sample Problem

Check out this table and let's build an exponential function:

Notice that f(x) changes by a product of 3. Each value is multiplied by 3 to get to the next value. This tells us it is an exponential function (compared to a linear function which would add or subtract a constant value).

So, what does that mean for me, you may ask? Well, it's pretty simple. What we need to know is: what happens at zero? f(0) = 9. Our initial value is 9. What are we multiplying each time by? 3. That means the base is 3. Hold on while we pull the rabbit out of the hat:

f(x) = 9(3)^x

Tada! Congratulations, we just built our first exponential function based on a table.