Think you’ve got your head wrapped around Continuity of Functions? Put your knowledge to
the test. Good luck — the Stickman is counting on you!
Q.
- Identify the picture(s) in which we can see what f is doing for all values of x in the window.
I.  y = 5x 3– 6x2 with -0.4 ≤ x ≤ 0.4
y = 5x 3– 6x2 with -0.4 ≤ x ≤ 0.4
II.  y = 5x3– 6x2 with -0.6 ≤ x ≤ 0.6
y = 5x3– 6x2 with -0.6 ≤ x ≤ 0.6
I only
II only
Neither I nor II
Both I and II
Q. Four different graphs of the function f(x) = 2x2 + 1 are shown below. Which picture best illustrates the fact that if x is within 0.06 of 2, then f(x) is within 0.5 of f(2) = 9?
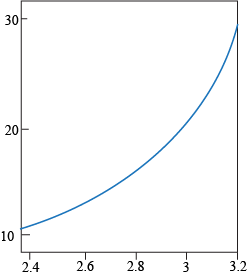
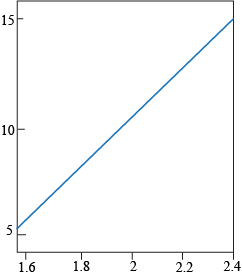
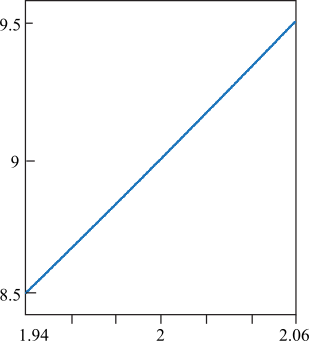
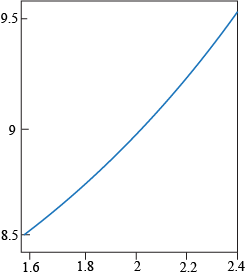
Q. Which statement is true for the function f shown below?

If x is within 0.5 of 0.5 then f(x) is within 0.5 of 1.5.
If x is within 0.5 of 2 then f(x) is within 0.5 of 3.
If x is within 0.5 of 3 then f(x) is within 0.5 of 1.
If x is within 0.5 of 3.5 then f(x) is within 0.5 of 1.25.
Q. We have a function f. We want f(x) to be within 0.5 of f(0). For which of the following functions do we have a guarantee that we can restrict x to find what we want? (x must be allowed to move the same distance from 0 in either direction, and x may not just be set equal to 0.)

III only
II and III
I and III
I, II, and III
Q. If f(x) = 4 – 2x then when |x – 1| < 0.5 we have a guarantee that |f(x) – 2| < 1. Identify c, ε, and δ as commonly used in the definition of continuity.
c = 2, ε = 1, δ = 0.5
c = 2, ε = 0.5, δ = 1
c = 1, ε = 1, δ = 0.5
c = 1, ε = 0.5, δ = 1
Q. Let f(x) = 3x + 1. Then f is continuous at 1 with f(1) = 4. Find the largest value of δ for which if x is within δ of 1, then f(x) is within 0.5 of 4.
0.16


1
Q. Let 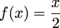 Then f is continuous at 4 with f(4) = 2. Find the largest value of δ for which if x is within δ of 4, then f(x) is within 0.25 of f(4).
Then f is continuous at 4 with f(4) = 2. Find the largest value of δ for which if x is within δ of 4, then f(x) is within 0.25 of f(4).
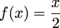 Then f is continuous at 4 with f(4) = 2. Find the largest value of δ for which if x is within δ of 4, then f(x) is within 0.25 of f(4).
Then f is continuous at 4 with f(4) = 2. Find the largest value of δ for which if x is within δ of 4, then f(x) is within 0.25 of f(4). 0.25
0.5
1
2
Q. In the formal definition of continuity at x = c,
ε describes how close we want f(x) and f(c), while δ describes how close x and c need to be.
δ describes how close we want f(x) and f(c), while ε describes how close x and c need to be.
ε and δ may be used interchangeably.
neither ε nor δ is used at all.
Q. If the function f is continuous at c, then
for some ε > 0 we can find a δ > 0 such that if |x – c| < δ then |f(x) – f(c)| < ε.
for some δ > 0 we can find an ε > 0 such that if |x – c| < δ then |f(x) – f(c)| < ε.
for every δ > 0 we can find an ε > 0 such that if |x – c| < δ then |f(x) – f(c)| < ε.
for every ε > 0 we can find a δ > 0 such that if |x – c| < δ then |f(x) – f(c)| < ε.
Q.
- Let
 , c = 0, and ε = 0.1.
, c = 0, and ε = 0.1.
Which is the largest value of δ such that if |x – c| < δ, then |f(x) – f(c)| < ε ?

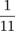
0.09
0.1