Answer
Don't panic at the instructions "derive the area formula." All this means is we need to use integration to find the area of the triangle, and we should get
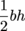
when we evaluate the integral at the end.
This problem is the same as problem 2 above except that we have letters instead of numbers for the side lengths.
Let y be the height of the slice at position x:
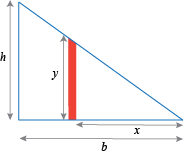
We have similar triangles again. The big triangle has height h and base b; the smaller triangle has height y and base x:
By similarity, we know that
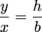
Since x is the variable of integration, we need to get the height (y) of the slice in terms of x:
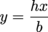
The area of the slice at position x is
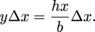
The variable x goes from 0 at the right tip of the triangle to b at the left edge of the triangle.
Taking the integral, we find that the area of the triangle is
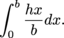
Let's evaluate this integral and see what we get:
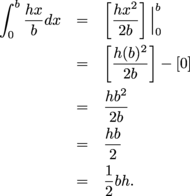
We found the area of the triangle using an integral, evaluated the integral, and got the formula for the area of a triangle. Finally, the long-awaited derivation of for the area of a triangle is ours. We have the power, so we might as well use it.