Trees: Binary Tree Height
Trees: Binary Tree Height
Ah, tree heights. The joy (or bane) of geometry students everywhere. Don't worry: we aren't about to make you take the sine of the shadow of a ladder to figure out how tall trees are in computer science. For one thing, it's really hard to balance a ladder against even the sturdiest of laptops (we've tried, it wasn't fun). For another, it doesn't help computer scientists with what they need the height for.
Plus, the way you do measure height is much less likely to get you in trouble with a particularly feisty squirrel. You will need to have a complete tree though.
A perfect binary tree with m nodes has a height equal to the floor of log2(m). (When we say floor, we just mean that we'll want to find a whole number and, if the number doesn't turn out to be whole, we'll always round down—never up.)
Not all trees are perfect. Actually, not many of them are. Just like the newest version of Barbie, trees come in all shapes and sizes.
As long as the binary tree is complete (meaning every level is completely filled from left to right before moving on down to the next one) then the height is easy to figure out.
Using this method, a complete binary tree with 6 nodes has a height equal to:
log2(6) = floor(2.58)
= 2
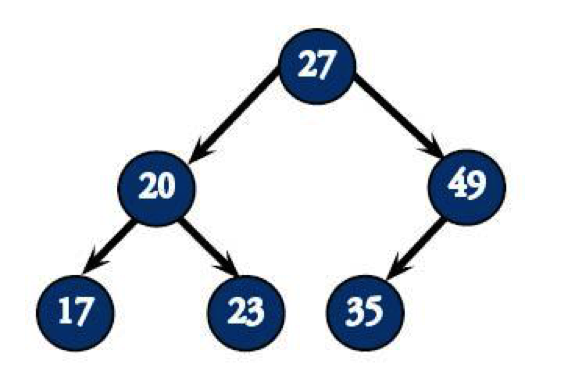
Notice how we said it would have a height of two but it actually has three levels? That's because height-counting starts at the 0th level, meaning the 27 at the root of this tree is on level 0 and 17 is on level 2.
If the tree is incomplete and/or severely unbalanced, then you might as well abandon all hope. There’s really no way to determine the height. A tree with a height of 7 could have only 8 nodes and a tree with a height of 3 could have 5. It’s like trying to estimate the height of a pine tree without any shadows, ladders, or Magic 8 balls. You don’t have the information you need. A tree has to be complete for all that formula stuff to work.
Once you've got the height, if you might also want to count the number of leaves, or nodes that don't have any other nodes coming off them. Just like everything else, it's much easier to calculate the number of leaves in computer science trees than in outside trees. Also, you don’t have to deal with all the creepy crawlies.
If you have a binary tree of height h, the maximum number of leaves it could possibly have is 2h. This is a tree at the height of its fully-foliated, binary glory. The tree could also be getting ready for winter, stubbornly holding back that one last leaf before it drops down to the next level. That means we have a lower bound, too. The number of leaves on any given tree of height h is somewhere between 1 and 2h.
That's cool, but sometimes you want to know how many total nodes a tree has. You can't guarantee any one number (unless the height's 0, of course), but since we're dealing with binary trees and each node can only branch twice, you can estimate a pretty decent range. At the very least, a complete tree of height h has to have 2h nodes. If that tree's also perfect, it could have as many as 2h + 1 – 1 nodes. That means the number of nodes could be anywhere between these two numbers:
2h ≤ nodes ≤ 2h + 1 – 1
For example, a complete tree of height 2 has to have at least 4 nodes (22), because if every node branches exactly twice at each level, that's the only number that would make the tree complete. Even so, the last level doesn't have to fill up every possible node space, so it can have as many as 7 ( which is 23 - 1) nodes. Similarly, a complete tree of height 5 has to have at least 32 nodes, but can have up to 63.
Non-complete trees? They could have as few as h nodes, making them essentially linked lists.
Values
Binary trees are great for searching if you organize things right. If you're smart, you can search through 1023 nodes in—at most—nine nodes. When you organize a tree so that everything to the left is less than the value of the node and everything to the right is greater than the value of the node, then you only need to search the height of the tree (max) to find any value.
When you use a tree to sort things, you can call.it a—wait for it—binary search tree, or a BST for short.
If, instead, you happen to be interested in an entire range of values that a certain BST might have, we only need to look as far left and as far right as the range of values. It’s like knocking on your friend Sam’s door and asking her mom whether she’s home instead of looking through the whole house to figure out that she isn't even there.
Also, you're much less likely to get mistaken for a burglar that way. Win-win.
Performing this sort of analysis—ideally before searching everywhere through a tree—is important because it can tell you if the number/value even has a chance of being in the tree. Why waste your time if it clearly isn't in the range of the tree?
For example, the tree below has nodes ranging from 15 to 75.
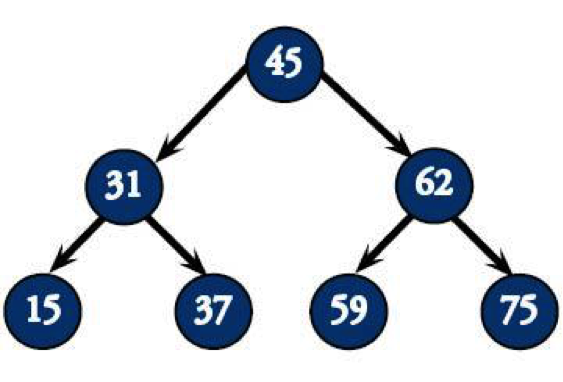
Searching for a number like 3 or 82 would be useless, since it's below or above the lowest or greatest value, which you can see since the leftmost leaf is 15 and the rightmost leaf is 75.
And don't even think about asking around for 3,594. You wouldn't even be in the right forest.
If you’re going to search a forest full of trees for one leaf, you'll want to make sure you start in the right forest, and then find the right tree.